Теоретичні основи евристичного підходу до встановлення тезаурусу навчальної дисципліни

Володимир Камишин

Олексій Рева

Сергій Завгородній

Лариса Сагановська

Анотація

В умовах інформаційного буму нагально актуальним є виріщення проблеми, з одного боку, структурної організації (ірхітектоніки) простору знань, що за світовими прогнозами має досягти у 2025 році 163 Zb. З іншого ж боку, йдеться про визначення тезаурусу певної галузі знань (чи певної навчальної дисципліни), тобто того повного і систематизованого набору даних, що вважається в інформатиці доcmатнім для людини-користувача або ЕОМ, щоби успішно орієнтуватися в цій галузі знань. І саме цей тезаурус має бути успішно опанованим навченими в межах відповідних навчальних програм.

Розглядаючи «дерево знань» як об’єкт, схожий навіть не на розгалужений кущ, а на баньян з кількома стовбурами, обґрунтовано теоретичну можливість і представлено математичну модель застосування методології евристичних рішень для «обрізання» зазначеного «дерева», а отже формування шуканих тезаурусів навчальних дисциплін.

Ключові слова: інформаційний бум; обмеженість ресурсів людини з опанування знаннями; евристичні рішення; тезаурус навчальної дисципліни.

Постановка проблеми

Бум інформаційних технологій, зокрема прогрес у методах збору, зберігання і обробки даних, призвів до накопичення величезних їх обсягів. За світовою статистикою, якщо у 2006 році обсяг інформації, вироблений людством за усю історію його існування, дорівнював 0,16 Zb (1 zettabyte (Zb)=1021 байт), то очікується, що у 2025 році він зросте до 163 Zb, що у 10 разів більше за показник 2016 року. Відповідну динаміку наочно ілюструє рис. 1.

Рис. 1. Світова динаміка зростання обсягів інформації

Наведене робить актуальним вирішення проблеми обробки, структуризації, аналізу, а отже й опанування інформації людиною-користувачем. Оскільки в протилежному випадку її величезний обсяг перетвориться у щось на кшталт інформаційного Демона Другого Порядку, описаного майже 50 років тому в «Кіберіаді» чудового польського фантаста С. Лема (Stanisław Herman Lem) (Лем, 1990).

Оскільки «слона вживають маленькими кусманчиками», то й знання варто опановувати певними «порціями», тому у контексті наших досліджень ідеться про необхідність науково-обґрунтованого визначення меж змістовного (знаннєвого) наповнення кожної навчальної дисципліни (НД), тобто формування її тезаурусу (від лат. thēsaurus – скарб, множина, скарбниця, що відтворює), під яким в інформатиці розуміють повний систематизований набір даних певної галузі знань, що дозволяє людині-користувачу або ЕОМ у ній успішно орієнтуватися. Тобто, йдеться ще й про внутрішню цілісність і завершеність тезаурусу. І зрозуміло, що знання, що виходять за межі тезаурусу, людина опановуватиме в процесі виробничої чи наукової діяльності.

Отже, порушується питання щодо науково-обґрунтованого «обрізання» відомого ще з біблейських часів «дерева знань» (рис. 2), яке, як видно з рис. 1, на сучасному етапі існування людства незвичайно активно, майже мультиплікативно, «кущиться». Причому автори погоджуються з думкою Джонардона Ганері (Jonardon Ganeri,), професора філософії Нью-Йоркського університету в Абу-Дабі, що «дерево знань варто уявляти як баньян, з його численним повітряним корінням, а не як яблуню (дерево з єдиним стволом)». Тому йдеться не лише про послідовно-паралельну взаємодію і доповнення знань, але ще й про їх позитивну інтерференцію та конвергенцію, що може бути ознакою та передумовою виникнення синергетичного ефекту.

Рис. 2. Ілюстрація біблейського «дерева знань», що кущиться

Аналіз досліджень і публікацій

На сьогодні вирішення проблеми обґрунтування тезаурусу НД (ТНД) дещо підмінюється формуванням змісту НД, що вирішуються методами педагогічного проєктування. Причому зміст НД формується, переважно, на основі багатого особистого досвіду науково-педагогічної праці його розробників. Тому, якщо реалізація відповідних результатів і призводить по позитивних наслідків, інколи навіть суттєвих, проте вони не є оптимальними через відсутність обґрунтованої науково-методологічної основи – моделі організації освітнього простору знань і інструментарію обрізання відповідного «дерева» для встановлення ТНД.

У праці (Камишин, Рева, Добровольська, 2016) обґрунтовано системно-кібернетичні основи формування простору знань в умовах інформаційного буму, що дозволяє розробити модель архітектоніки знань, а отже побудувати відповідне «дерево», що кущиться, з якого й має вирізатися тезаурус певної НД чи галузі знань (рис. 3). Однак, при цьому не обґрунтовується ані глибина, ані ширина зазначеного «обрізання», що й має бути предметом спеціальних досліджень. З аналізу праць за темою дослідження випливає можливість застосування з зазначеною метою методології теорії евристичних рішень.

Архітектоніка «дерева знань»: гіпотетичний приклад формування тезаурусу знань з певної навчальної дисципліни

Постановка завдання дослідження. Виходячи з вищенаведеного, метою цієї публікації є наукове обґрунтування застосування методології теорії евристичних рішень (ЕР) для формування ТНД.

Виклад основного матеріалу

Сутність застосування евристичних моделей ПР для обрізання «дерева знань» і формування ТНД. Насамперед визначимося з відповідною термінологією.

У наших дослідженнях уважатимемо, що прийняття рішень (УР) – це цілеспрямований акт емоційно-вольового вибору експертом (групою експертів) певної кількості гілок (за потреби й стовбурів, якщо йдеться про «баньян») «дерева знань» для формування ТНД шляхом перетворення вихідної інформації, коли ситуація організації архітектоніки знаннєвого простору невизначена.

Водночас ЕР – це алгоритм вибору певної кількості гілок (за потреби й стовбурів, якщо йдеться про «баньян») «дерева знань» для формування ТНД, що базується на досвіді експерта (групи експертів) та інтуїції, осяянні та синергії, не є гарантовано точними чи оптимальними, але достатні для вирішення поставленої задачі. Типовими умовами застосування ЕР є дефіцит часу на розв’язання проблемної ситуації і перевантаження інформацією, що ускладнює процес її обробки.

Спираючись на попередні дослідження нашої проблеми, розглянемо зміст евристичних методів та рішень на прикладі обрізання «дерева знань» для створення тезаурусу певної НД. При цьому матимемо на увазі думку піонерів ЕР А. Ньюелла (Allen Newell) та Г. Саймон (Herbert A. Simon), які, розглядаючи розгалужені процеси, зауважували про те, що коли суб’єкт, який вирішує задачу, стикається з групою альтернатив, звичайний евристичний прийом полягає у виявленні з самого початку можливих шляхів за допомогою відносно доступного тесту.

Отже, вважатимемо, що загальна кількість гілок «дерева знань», що з’являються на T-му етапі, дорівнює N^T.

Якщо маємо граф виду рис. 3, що містить N альтернатив у кожному корені, то він має довжину T і один правильний шлях до мети, то при випадкових пробах буде потрібно зробити у середньому (0,5⋅N)^T проб. У тому ж графі, якщо евристичний тест дозволить відкинути як безрезультатні половину альтернатив у кожному корені і здійснити випадковий пошук, кількість проб зменшиться до 0,5⋅(0,5⋅N)^T, тобто, у 2 рази, і т.д.

Як бачимо, рис. 3 ілюструє, як сходяться знання, поняття з різних навчальних дисциплін і наукових напрямків у деякий знаннєвий простір, званий тезаурусом конкретної НД. Обрізання цього розгалуженого куща відбувається шляхом застосування того або іншого тесту. Внаслідок цього одержується вже усічений процес, що кущиться, в якому ефективність пошуку рішень щодо залучення у тезаурус певної навчальної інформації оцінюється так: Нехай, m₁, m₂, …, m_(T+1) - кількість усічених коренів процесу, що кущиться на 1-му, 2-му, ..., T-му , T+1-му етапах рішення, а N - кількість операцій, що застосовуються. Тоді кількість гілок на цих етапах складе відповідно:

	(1)

Якщо на деякому етапі, скажімо, на T-му, Ви досягнете рішення, то на наступному, T+1-му, етапі всі гілки необхідно усікти, тобто, l_(T+1)=0.

Позначимо загальну кількість відсічених гілок – через M, а загальну кількість гілок, що залишилися, – через L. Тоді

	(2)

Складаючи рівняння (1), отримуємо

	(3)

Або з врахуванням виразу (1), прийдемо до результату

	(4)

Вважаючи, що кількість гілок, яка залишилась, може бути інтерпретованою як довжина шляху, що веде до рішення, одержаний результат можна інтерпретувати у такий спосіб: довжина шляху, що веде до рішення, залежить від співвідношення кількості відсічених коренів і кількості застосованих операцій.

Розуміючи у подальшому під ефективністю рішення E(T) співвідношення довжини шляхів, що ведуть до рішення, без використання L^* і з використанням L того чи іншого тесту (знання), одержимо:

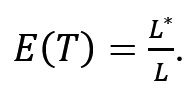	(5)

Якщо тест не використовувати, то кількість шляхів до рішення буде максимальною і визначатиметься так:

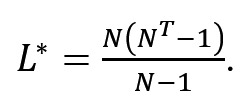	(6)

Підставляючи формули (4) і (6) до виразу (5) одержимо

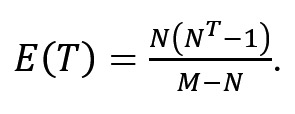	(7)

Знайдемо граничні значення M, а через них й E(T).

1. M_min існує лише тоді, коли на кожному з T етапів є тільки один шлях, а на (T+1)-му етапі немає жодного шляху, оскільки рішення вже знайдено, тобто:

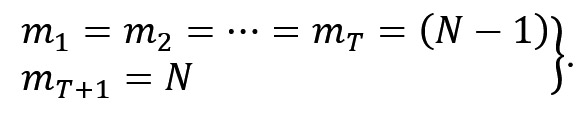	(8)

Тоді маємо, що

	(9)

2. M_max можливо, коли на кожному з T етапів мають місце всі шляхи, а на (T+1)-му етапі всі шляхи відсічені, тобто

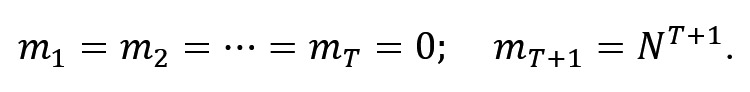	(10)

Звідси маємо, що

	(11)

Підставляючи одержані значення M_min і M_max до рівності (2), матимемо:

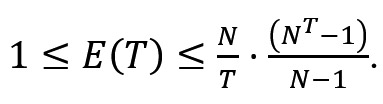	(12)

Підрахуємо далі ефективність рішення при використанні ієрархічної системи рішення. Нехай передостанній рівень ієрархічної системи створює p підцілей (і, таким чином, p етапів), що об’єднують по T' операцій останнього рівня. Тоді T=pT'.

Загальна кількість гілок, що ведуть до кожної з підцілей, у відповідності із раніш наведеним буде N(N^(T'-1) )/(N-1), а всього

	(13)

Порівнюючи останній вираз (13) із загальною кількістю шляхів до рішення, матимемо:

	(14)

Або, враховуючи, що N^T>>1 і N^T'>>1,

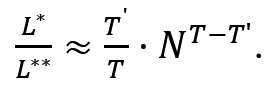	(15)

На завершення зауважимо, що дослідження евристичних стратегій, що застосовуються при вирішенні наукових проблем, а також проблем, які виникають у колективних іграх або в процесі ПР іншого роду, значно розширюють спектр знань окремої людини.

Висновки:

1. Ця стаття є природнім розвитком попередніх досліджень авторів з застосування методології теорії графів для формування організаційної структури (архітектоніки) взаємодії дидактичних одиниць (ДО) у багатовимірному просторі знань.

2. Обґрунтовано, що, враховуючи взаємну послідовно-паралельну залежність та доповнення знань, відповідне «дерево» має розглядатися не просто як розгалужений кущ, а як баньян, з його численним повітряним корінням.

3. Виходячи з мети дослідження розкрито зміст дефініцій прийняття рішення (УР) та евристичне рішення (ЕР).

4. Спираючись на отримувану в вищенаведений спосіб архітектоніку ДО, уперше аналітично обґрунтовано і математично заформалізовано застосування евристичних методів УР для встановлення ТНД, зокрема обрізання «дерева знань», яке активно кущиться, що й сприяє формуванню тезаурусу певної галузі знань або НД.

5. Подальші дослідження з розвитку кібернетичної системно-інформаційної методології у педагогіці слід проводити у таких напрямах (не ранжуючи):

– обґрунтування моделі припинення навчання;

– встановлення критеріїв компетентності учасників освітньо-виховного процесу, спираючись на показники і характеристики впливу людського чинника на УР;

– розроблення методології усунення «статистичної похибки того, хто вижив» у групових рішеннях учасників ОВП тощо.

Використані джерела

Kремень, В. Г., Ільїн, В.В. (2012). Синергетика в освіті: контекст людиноцентризму. Педагогічна думка.

Камишин, В. В., Рева, О.М., Добровольська, Н.А. (2016). Системно-кібернетичні основи організації простору знань у дидактиці в умовах інформаційного буму. Вища школа, 9, 103‒117.

Кремень, В. Г. (2014). Проблеми якості української освіти в контексті сучасних цивілізаційних змін. Педагогіка і психологія, 4, 5–10.

Купенко, В. О. (2015). Педагогічні проекти: навчальний посібник. Сумський державний університет.

Лем, С. (1990). Подорож шоста, або як Трурль і Кляпавцій створили Демона Другого Порядку, аби розбійника Морданя перемогти. Кіберіада (І.І. Сварник, Пер. з польськ.) (сс.182‒196). Видавництво художньої літератури «ДНІПРО».

Рева, О.М., Камишин, В.В., та ін. (2019). Методи і моделі кваліметрії синергетичного ефекту у дидактиці: монографія. ІОД НАПН України.

Савельєва, Н.М. (Ред.) (2017). Навчально-методичне забезпечення освітніх компонентів: довідник для педагогічних та науково-педагогічних працівників. ПНПУ імені В. Г. Короленка.

Шевченко, І. (2010). Педагогічне проєктування та його складові. Наукові записки Кіровоградського державного педагогічного університету імені Володимира Винниченка. Педагогічні науки, 91, 256‒260.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.